Kesimbangan lini bertujuan mengurangi waktu menganggur stasiun kerja dan mengurangi persediaan barang setengah jadi (work in progress). Misal, stasiun kerja 2 walaupun sedang menganggur tidak dapat melakukan proses pengerjaaan jika pada proses pengerjaan stasiun kerja 1 belum selesai. Keseimbangan lini bertujuan menyeimbangkan beban kerja pada stasiun-stasiun kerja.
Berikut merupakan contoh meyeimbangkan beban kerja menggunakan pemrograman linier yg akan dituangkan kedalam bentuk soal.
PT. X mengalami kenaikan permintaan lemari yg sangat tinggi pada bulan Mei. Permintaan lemari tersebut terdiri atas berbagai tipe lemari. Di bawah ini merupakan permintaan lemari untuk masing-masing tipe.
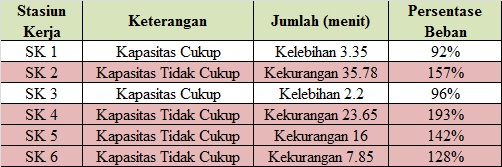
Stasiun Kerja 2, 4, 5 dan 6 tidak memiliki kapasitas yang cukup dalam memenuhi permintaan lemari bulan Mei. Masing-masing kapasitas memiliki beban kerja yang tidak seimbang seperti data di bawah ini.
Dalam upaya mengurangi ketidakcukupan kapasitas pada beberapa stasuin kerja tersebut, perusahaan hanya bisa menambah kapasitas 49.5 menit pada bulan Mei. Kapasitas tersebut berasal dari jam kerja lembur.
Permasalahnnya ?
Berapa banyak kapasitas yg harus dialokasikan pada stasiun kerja yg kekurangan kapasitas agar persentase beban kerja dapat seimbang, sehingga dapat mengurangi atau bahkan menghilangkan persediaan barang setengah jadi (work in progress).
Jawab :
SK yg akan diseimbangkan beban kerjanya adalah SK 2, 4, 5, dan 6. Beban kerja SK tersebut haruslah sama persentasenya.
Menentukan Variabel :
X1 = kapasitas yg ditambahkan pada SK 2
X2 = kapasitas yg ditambahkan pada SK 4
X3 = kapasitas yg ditambahkan pada SK 5
X4 = kapasitas yg ditambahkan pada SK 6
Bentuk Dasar :
(Kapasitas Tersedia+X)/(Kapasitas yg Dibutuhkan) = Persentase beban yg bisa ditangani
(Kapasitas Tersedia SK2+X1)/(Kapasitas yg Dibutuhkan SK2) = (Kapasitas Tersedia SK4+X2)/(Kapasitas yg Dibutuhkan SK4) = (Kapasitas Tersedia SK5+X3)/(Kapasitas yg Dibutuhkan SK5) = (Kapasitas Tersedia SK6+X4)/(Kapasitas yg Dibutuhkan SK6)
(63.12+X1)/98.9 = (25.5+X2)/49.15 = (37.9+X3)/53.9 = (28.35+X4)/36.2
Formulasi
Max Z = X1 + X2 + X3 + X4
1. Beban SK2 harus samadengan SK4 (63.12+X1)/98.9 = (25.5+X2)/49.15
2. Beban SK4 harus samadengan SK5 (25.5+X2)/49.15 = (37.9+X3)/53.9
3. Beban SK2 harus samadengan SK6 (37.9+X3)/53.9 = (28.35+X4)/36.2
Merubah formulasi di atas menjadi bentuk pemrograman linier dengan perkalian silang.
Formula 1
(63.12 x 49.15) + (X1 49.15) = (25.5 x 98.9) + (X2 98.9)
3102.348 + 49.15X1 = 2521.95 + 98.9X2
(3102.348 - 2521.95) + 49.15X1 - 98.9X2 = 0
580.398 + 49.15X1- 98.9X2 = 0
49.15X1 - 98.9X2 = -580.398
Formula 2
(25.5 x 53.9) + (X2 53.9) = (37.9 x 49.15) + (X3 49.15)
1374.45 + 53.9X2 = 1862.785 + 49.15X3
(1374.45 - 1862.785) + 53.9X2 - 49.15X3 = 0
-488.335 + 53.9X2 - 49.15X3 = 0
53.9X2 - 49.15X3 = 488.335
Formula 3
(37.9 x 36.2) + (X3 36.2) = (28.35 x 53.9) + (X4 53.9)
1371.98 + 36.2X3 = 1528.065 + 53.9X4
(1371.98 - 1528.065) + 36.2X3 - 53.9X4 = 0
-156.085 + 36.2X3 - 53.9X4 = 0
36.2X3 - 53.9X4 = 156.085
4. Jumlah pertambahan kapasitas tidak lebih dari 49.5
X1 + X2 + X3 + X4 <= 49.5
Formulasi Keseluruhan Adalah :
Max X1 + X2 + X3 + X4
49.15X1 - 98.9X2 = -580.398
53.9X2 - 49.15X3 = 488.335
36.2X3 - 53.9X4 = 156.085
X1 + X2 + X3 + X4 <= 49.5
Berikut hasil optimal menggunakan software Lindo


Nilai tujuan optimal yg didapatkan adalah 49.5 dengan nilai optimal variabel x1=21.75169, x2=16.678398, x3= 8.354642, x4= 2.71527.
Hasil yg didapatkan adalah setiap SK (SK1, SK2, SK3, dan SK4) dapat menangani beban kerja sebanyak 86%, dan sisa 14% beban yg belum bisa ditangani.
Contoh perhitungan:
SK2 = (63.12+21.75169)/ 98.9 = 86%




No comments:
Post a Comment